Python numPy:
NumPy is the core library for scientific computing in python. It provides a high-performance multidimensional array object, and tools for working with these arrays. Numpy can also be used as an efficient multi-dimensional container of generic data. Moreover, it is fast and reliable. Numpy functions return either views or copies.
Python numpy Array:
NumPy arrays are a bit like Python lists, but still very much different at the same time. A NumPy array is a central data structure of the numpy library ("Numeric Python" or "Numerical Python").
Create a numPy Array:
Simplest way to create an array in numpy is to use Python List
Or
Mathematical Operations on an Array:
Shape and dtype of Array:
Shape: is the shape of the array
Dtype: is the datatype. It is optional. The default value is float64
np.zeros and np.ones:
You can create a matrix full of zeroes or ones using np.zeros and np.one commands respectively. It can be used when you initialized the weights during the first iteration in TensorFlow and other statistic tasks.
The syntax is:
numpy.zeros(shape, dtype=float, order='C')
numpy.ones(shape, dtype=float, order='C')
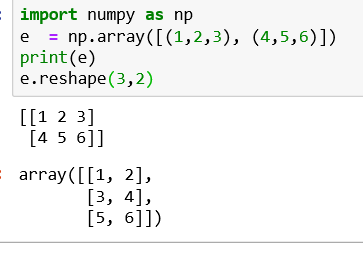
numpy.reshape() and numpy.flatten() :
Reshape Data: In some occasions, you need to reshape the data from wide to long. You can use the reshape function for this.
The syntax is
numpy.reshape(a, newShape, order='C')
Here,
a: Array that you want to reshape
newShape: The new desires shape
Order: Default is C which is an essential row style.
Flatten Data: When you deal with some neural network like convnet, you need to flatten the array. You can use flatten().
The syntax is
numpy.flatten(order='C')
Here,
Order: Default is C which is an essential row style.
numpy.hstack() and numpy.vstack():
With hstack you can appended data horizontally. This is a very convenient function in Numpy.
With vstack you can appened data vertically.
Generate Random Numbers: To generate random numbers for Gaussian distribution use
numpy.random.normal(loc, scale, size)
Here,
Loc: the mean. The center of distribution
scale: standard deviation.
Size: number of returns
numpy.asarray() :
The asarray() function is used when you want to convert an input to an array. The input could be a lists, tuple, ndarray, etc.
Syntax:
numpy.asarray(data, dtype=None, order=None)[source]
Here,
data: Data that you want to convert to an array
dtype: This is an optional argument. If not specified, the data type is inferred from the input data
Order: Default is C which is an essential row style. Other option is F (Fortan-style)
Matrix is immutable. You can use asarray if you want to add modification in the original array.
Example:
If you want to change the value of the third rows with the value 2np.
asarray(A): converts the matrix A to an array
[2]: select the third rows
numpy.arange() :
Sometimes, you want to create values that are evenly spaced within a defined interval. For instance, you want to create values from 1 to 10; you can use numpy.arange() function.
Syntax:
numpy.arange(start, stop,step)
Here,
Start: Start of interval
Stop: End of interval
Step: Spacing between values. Default step is 1
numpy.linspace() and numpy.logspace():
Linspace: Linspace gives evenly spaced samples.
Syntax:
numpy.linspace(start, stop, num, endpoint)
Here,
Start: Starting value of the sequence
Stop: End value of the sequence
Num: Number of samples to generate. Default is 50
Endpoint: If True (default), stop is the last value. If False, stop value is not included.
If you do not want to include the last digit in the interval, you can set endpoint to false
np.linspace(1.0, 5.0, num=5, endpoint=False)
LogSpace: LogSpace returns even spaced numbers on a log scale. Logspace has the same parameters as np.linspace.
Syntax:
numpy.logspace(start, stop, num, endpoint)
Finally, if you want to check the size of an array, you can use itemsize
Indexing and Slicing NumPy Arrays:
Slicing data is trivial with numpy. We will slice the matrices "e". Note that, in Python, you need to use the brackets to return the rows or columns
Note: The values before the comma stand for the row. The value on the rights stands for the columns. If you want to select a column, you need to add: before the column index.: means you want all the rows from the selected column.
To return the first two values of the second row. You use: to select all columns up to the second
NumPy Statistical Functions:
NumPy has quite a few useful statistical functions for finding minimum, maximum, percentile standard deviation and variance, etc from the given elements in the array.
numpy.dot():
Dot Product: Numpy is powerful library for matrices computation. For instance, you can compute the dot product with np.dot
Syntax:
numpy.dot(x, y, out=None)
Here,
x,y: Input arrays. x and y both should be 1-D or 2-D for the function to work
out: This is the output argument. For 1-D array scalar is returned. Otherwise ndarray.
NumPy Matrix Multiplication with np.matmul() :
The Numpu matmul() function is used to return the matrix product of 2 arrays. Here is how it works1) 2-D arrays, it returns normal product2) Dimensions > 2, the product is treated as a stack of matrix3) 1-D array is first promoted to a matrix, and then the product is calculated
numpy.matmul(x, y, out=None)
Here,
x,y: Input arrays. scalars not allowed
out: This is optional parameter. Usually output is stored in ndarray
Determinant:
Last but not least, if you need to compute the determinant, you can use np.linalg.det(). Note that numpy takes care of the dimension.
Importing and Exporting Of Files:
import numpy as np
np.loadtxt (file.txt) # imports from a text file
np.savetxt (‘file.txt’,arr,delimiter= ’ ’) #writes to a text file